广义斯托克斯公式

我们在高数里面学了蛮多微积分定理的, 比如以下定理

  • Stoke’s 定理

∮∂DF→⋅dr→=∬D(▽×F→)⋅dA→\oint_{\partial D}\overrightarrow{F}\cdot d \overrightarrow{r} = \iint_{D}(\triangledown\times \overrightarrow{F})\cdot d \overrightarrow{A}

  • 高斯定理

∬∂DF→⋅dA→=∭D(▽⋅F→)dV\iint_{\partial D}\overrightarrow{F}\cdot d \overrightarrow{A}=\iiint_{D}(\triangledown\cdot \overrightarrow{F})dV

  • 格林公式

∮∂DPdx+Qdy=∬D(∂Q∂x−∂P∂y)dA\oint_{\partial D}Pdx + Qdy=\iint_{D}\left( \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \right)dA

  • 甚至是牛顿-莱布尼兹公式

f(a)−f(b)=∫baf′(x) dxf(a)-f(b) = \int _{b}^a f'(x) \, dx

先不论其他的, 至少在格林公式上肯定听过一个解释, 就是无数微小的线积分构成整个区域的线积分, 然后根据基本的微积分思想, 转化为平面的二重积分, 示意图想必都很熟悉了

但其实你们观察这些形式, 说不定你们就能发现, 其实他们都是一个形式, 或者不用观察, 想一想, 对一块封闭区域的积分, 是不是就是里面所有微小扰动的总和, 这就是广义斯托克斯公式

∫D dω=∫∂D ω\int _{D} \, d \omega=\int _{\partial D} \, \omega

可以再对照一下前面的几个公式

f(b)−f(a)⏟∫∂Dω=∫abf′(x)dx⏟∫Ddω\underbrace{f(b) - f(a)}_{\int_{\partial D} \omega} = \underbrace{\int_a^b f'(x) dx}_{\int_D d\omega}

∮∂DPdx+Qdy⏟∫∂Dω=∬D(∂Q∂x−∂P∂y)dA⏟∫Ddω\underbrace{\oint_{\partial D} P dx + Q dy}_{\int_{\partial D} \omega} = \underbrace{\iint_D \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) dA}_{\int_D d\omega}

∬∂DF⃗⋅dA⃗⏟∫∂Dω=∭D(∇⋅F⃗) dV⏟∫Ddω\underbrace{\iint_{\partial D} \vec{F} \cdot d\vec{A}}_{\int_{\partial D} \omega} = \underbrace{\iiint_D (\nabla \cdot \vec{F}) \,dV}_{\int_D d\omega}

∮∂DF⃗⋅dr⃗⏟∫∂Dω=∬D(∇×F⃗)⋅dA⃗⏟∫Ddω\underbrace{\oint_{\partial D} \vec{F} \cdot d\vec{r}}_{\int_{\partial D} \omega} = \underbrace{\iint_D (\nabla \times \vec{F}) \cdot d\vec{A}}_{\int_D d\omega}

是不是看出来了什么, 直观的解释就是在边缘上对某个函数的积分就等于在内部对这个函数变化率的积分, 边缘与内部问题相信你们应该很清晰了, 这里我们来看这个 ω→dω\omega \to d \omega 的问题, 这里有一个符号 dd, 也就是平常经常接触的外微分算子

这里我们先引入一个新的运算, 楔积‘ ∧\wedge ‘, 也叫外积, 这里在 R3\mathbb{R}^3 下的具体运算规则如下

dx∧dx=0, dy∧dy=0, dz∧dz=0dx∧dy=−dy∧dx, dx∧dy=−dy∧dzdy∧dz=−dz∧dy\begin{align*} dx \wedge dx &= 0,\ dy \wedge dy = 0,\ dz \wedge dz = 0 \\ dx \wedge dy &= -dy \wedge dx ,\ dx \wedge dy = -dy \wedge dz \\ dy \wedge dz &= -dz \wedge dy \end{align*}

诶这里你们可能会联想到叉积 ×\times, 这和叉积的定义很相似啊对吧, 交换次序后是反方向, 与自身的积是 0, 这里其实是三维空间的楔积和叉积是同构的, 不过吧, 叉积只是三维空间的定义, 虽然平时可能就只在三维空间里面使用(其实压根不会用吧), 但楔积作为一个需要扩展到其它维度的概念, 或许将其理解为其真正的含义会好点

示意图

这图表示的就挺清楚的, 我们都学过旋转的方向表示, 所以楔积就是表示的两个矢量所构成平面的, 诶那么那么, 这个矢量又是什么, 向量? 那三个矢量的楔积又怎么解释

所以这里的矢量其实应该理解成一个体积元, 也就是某个维度的微元, 也就是向高维度推广的所在了, 我们回到低维, 来看我们熟悉的一维微元 dxdx, 他代表了指向 xx 轴正向的一个微小线段, 那与另一个一维微元 dydy 的楔积就是一个有向面积

广义的体积元是什么, 你想想三维空间里面体积能做到什么, 把某个区域填满对吧, 所以一维的 dxdx 能把一段 xx 周方向的线段填满, 而二维平面的面积微元能把一个面填充完整, 而高维度的也一样, 所以楔积的本质是什么, 就是一种升维, 也就是我们需要一个更加高维度的体积元, 这就可以增加额外体积元带来的那一部分维度

但这是不是少了点什么, 线积分 →\to 面积分, 然后呢, 你还记得吗, 楔积是有向的, 这个方向意味着什么, 用最熟悉的格林公式来看

∮∂DPdx+Qdy=∬D(∂Q∂x−∂P∂y)dA\oint_{\partial D}Pdx + Qdy=\iint_{D}\left( \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \right)dA

你看到了什么, 这不就是 dx,dy→dxdydx, dy\to dxdy 吗, 线微元变成面微元, 这好像与方向无关啊, 这里我们就要谈谈这个微元的另外的重要, 这里看似无关, 其实隐含了一个条件, 第一个式子化为第二个式子之后, 其参照系是不变的, 也可以理解为 dxdx 和 dydy 的方向是固定的, 所以这两个量固定之后, 作为 dA=dxdydA=dxdy 这个量的方向也是固定的, 也就是说所谓的微元 dxdx 是一个绝对的, 客观的存在, 你在空间中定义一个微元 dxdx, 它不会因为你转身而跟着你转身, 这算是一个很哲学的概念吧我觉得, 毕竟人至始至终对事物的物理层面的观察都有一个参照系, 哪怕是绝对也有一个绝对参照系, 好吧扯远了, 总之这个绝对性其实有很多说法, 在这里也就奠定了你的 dAdA 的方向一定是固定的, 与 dxdx 和 dydy 是直接相关的

好我们来看外微分算子 dd , 你现在思考一个问题, 函数和函数微元之间有什么关系, 也就是 ω\omega 和 dωd \omega 之间, 想到了吗, 就是变化率, 你们真理解变化率是什么吗, 我们先回到函数的概念, 因为我们需要推广到高维, 所以你们原来的理解可能会与我描述的不同, 所以希望你能重新接受这个概念, 我们先来看些函数图像, 按照之前讲的微元的定义, 你们想一想所谓有向体积元, 再重新想一下函数的定义, 并想想按照你们的定义这些是几维

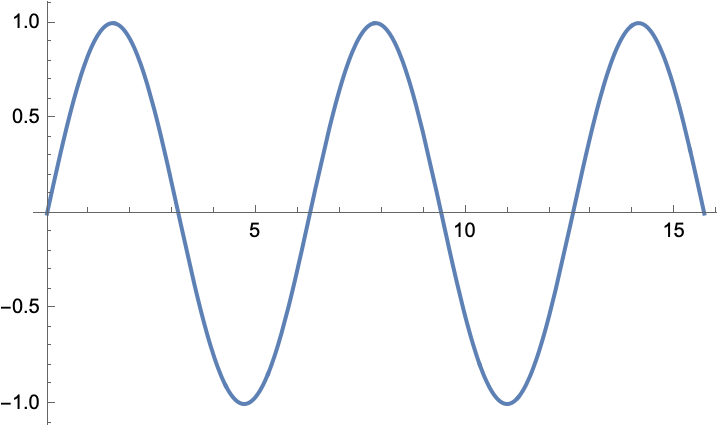
upgit_20250831_1756621847.png

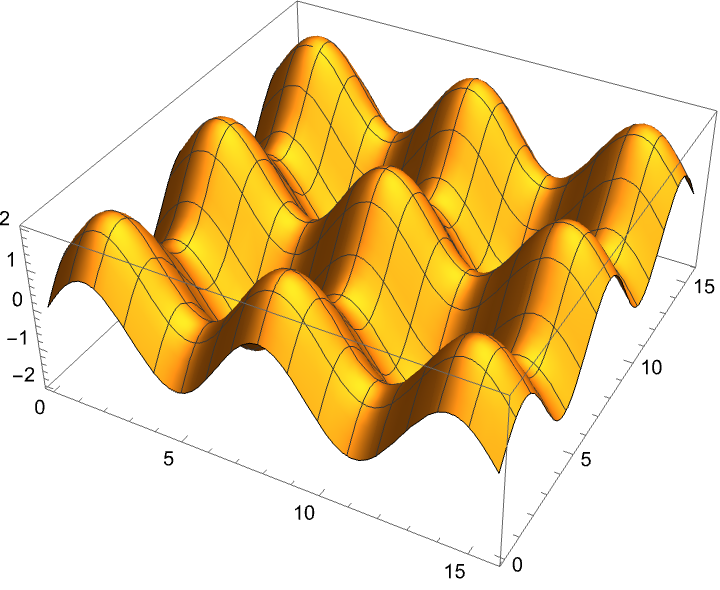
upgit_20250831_1756621942.png

想完了吗, 没思考出来一个确切的结果那就别往下看, 至少凭个感觉说说这是几维的

其实这就要提到另一个概念, 那就是内在维度 (Intrinsic dimension), 按照之前的定义, 第一个图的体积元是什么, 你可以想想我们是怎么对第一张图进行积分的, ∫f(x) dx\int f(x) \, dx, 那体积元是什么, dxdx, 对吧, 第二个图同理, 也就是 dxdydxdy, 诶这里我们发现, 这里好像就是一个体积元对应着一个值, 方向也是体积元可以决定的, 诶, 这个函数的表述不就出来了吗, 就是描述在每个构成整个空间的体积元的强度, 所以是几维, 对吧, 一个是一维, 一个是二维, 当然你也可以辩解说强度不是也是一个维度吗, 那太对了, 有这个想法说明你已经一定程度上深入了函数的本质

那么我们再来看变化率, df(x)df(x), 你发现什么, 这玩意的维度没变, 描述的就是各个体积元之间强度的变化, 是不是察觉到了什么, 我们之前所说的扰动是什么意思, 再看这个公式

∫D dω=∫∂D ω\int _{D} \, d \omega=\int _{\partial D} \, \omega

扰动不就是原函数的微分吗, 所以对区域边缘的函数积分就是对这个区域内部的函数微分的积分, 直接对最简单的牛顿莱布尼兹公式进行描述不就是微分(扰动)的累积(线积分)就是原函数在这个区间端点的差吗, 其他的你们可以自行描述一下, 总之就是这个感觉

OK 我们概念搞清楚了, 那么一切就变得很简单了, 回顾一下楔积的计算规则, 我们来试试推导一下 Stoke’s 定理

∮∂DF→⋅dr→=∮Pdx+Qdy+Rdz=(∂P∂xdx+∂P∂ydy+∂P∂zdz)∧dx+(∂Q∂xdx+∂Q∂ydy+∂Q∂zdz)∧dy+(∂R∂xdx+∂R∂ydy+∂R∂zdz)∧dz=(∂R∂y−∂Q∂z)dydz+(∂P∂z−∂R∂x)dzdx+(∂Q∂x−∂P∂y)dxdy=∬D(▽×F→)⋅dA→\begin{align*} \oint_{\partial D}\overrightarrow{F}\cdot d \overrightarrow{r} &=\oint Pdx+Qdy+Rdz \\ &=\left( \frac{\partial P}{\partial x}dx+\frac{\partial P}{\partial y}dy+\frac{\partial P}{\partial z}dz \right)\wedge dx+\left( \frac{\partial Q}{\partial x}dx+\frac{\partial Q}{\partial y}dy+\frac{\partial Q}{\partial z}dz \right)\wedge dy+\left( \frac{\partial R}{\partial x}dx+\frac{\partial R}{\partial y}dy+\frac{\partial R}{\partial z}dz \right)\wedge dz \\ &=\left( \frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z} \right)dydz+\left( \frac{\partial P}{\partial z}-\frac{\partial R}{\partial x} \right)dzdx+\left( \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} \right)dxdy\\ &= \iint_{D}(\triangledown\times \overrightarrow{F})\cdot d \overrightarrow{A} \end{align*}

很简单吧, 你们可以自己试试推一下其他几个公式

后记 (碎碎念碎碎念)

其实本来想分分点, 但又不知道在哪里中断好, 毕竟一环套一环, 哎反正也没人看, 其实吧, 感觉不懂的人也用不到这些, 背个公式就可以解决常用维度的东西了, 懂的那也没看的必要不是, 而且这里表述也不知道合不合规范, 也算是自己整理吧

感觉大学课程的编排就是一坨, 不过也不是人人非得要刨根问底不可, 再者刨根问底也是没完没了了的, 就很迷茫啊, 你知道需要改变, 但你知道找到一个改变的方向有多难吗, 所以有时候我会去追求一个统一性的概念, 事物的所谓本质, 或许只要不断解构, 就可以找到一切的, 也不能说一切吧, 就是基础, 至少是一部分的, 所以我会很看重定义, 就相当于在高塔上打了个钉子, 即使不在地表也能起到支撑作用

但可笑的是很多东西的本质和你想的完全不一样, 都说理科很灵活, 其实真正灵活的不在理科

参考

维基百科: 外代数

《数学分析教程》